隐藏网站的wordpress属性新型网络搜索引擎

---

---

[蓝桥杯 2022 国 A] 环境治理

题目链接

https://www.luogu.com.cn/problem/P8794

题目描述

LQ 国拥有 $n$ 个城市，从 $0$ 到 $n-1$ 编号，这 $n$ 个城市两两之间都有且仅有一条双向道路连接，这意味着任意两个城市之间都是可达的。每条道路都有一个属性 $D$，表示这条道路的灰尘度。当从一个城市 A 前往另一个城市 B 时，可能存在多条路线，每条路线的灰尘度定义为这条路线所经过的所有道路的灰尘度之和，LQ 国的人都很讨厌灰尘，所以他们总会优先选择灰尘度最小的路线。

LQ 国很看重居民的出行环境，他们用一个指标 $P$ 来衡量 LQ 国的出行环境，$P$ 定义为：

$$P=\sum _{i=0}^{n-1}\sum _{j=0}^{n-1}d(i,j)$$

其中 $d(i,j)$ 表示城市 $i$ 到城市 $j$ 之间灰尘度最小的路线对应的灰尘度的值。

为了改善出行环境，每个城市都要有所作为，当某个城市进行道路改善时，会将与这个城市直接相连的所有道路的灰尘度都减少 $1$，但每条道路都有一个灰尘度的下限值 $L$，当灰尘度达到道路的下限值时，无论再怎么改善，道路的灰尘度也不会再减小了。

具体的计划是这样的：

• 第 $1$ 天，$0$ 号城市对与其直接相连的道路环境进行改善；
• 第 $2$ 天，$1$ 号城市对与其直接相连的道路环境进行改善；

……

• 第 $n$ 天，$n-1$ 号城市对与其直接相连的道路环境进行改善；
• 第 $n+1$ 天，$0$ 号城市对与其直接相连的道路环境进行改善；
• 第 $n+2$ 天，$1$ 号城市对与其直接相连的道路环境进行改善；

……

LQ 国想要使得 $P$ 指标满足 $P\le Q$。请问最少要经过多少天之后，$P$ 指标可以满足 $P\le Q$。如果在初始时就已经满足条件，则输出 $0$；如果永远不可能满足，则输出 $-1$。

输入格式

输入的第一行包含两个整数 $n,Q$，用一个空格分隔，分别表示城市个数和期望达到的 $P$ 指标。

接下来 $n$ 行，每行包含 $n$ 个整数，相邻两个整数之间用一个空格分隔，其中第 $i$ 行第 $j$ 列的值 $D_{i,j}(D_{i,j}=D_{j,i},D_{i,i}=0)$ 表示城市 $i$ 与城市 $j$ 之间直接相连的那条道路的灰尘度。

接下来 $n$ 行，每行包含 $n$ 个整数，相邻两个整数之间用一个空格分隔，其中第 $i$ 行第 $j$ 列的值 $L_{i,j}(L_{i,j}=L_{j,i},L_{i,i}=0)$ 表示城市 $i$ 与城市 $j$ 之间直接相连的那条道路的灰尘度的下限值。

输出格式

输出一行包含一个整数表示答案。

样例 #1

样例输入 #1

3 10
0 2 4
2 0 1
4 1 0
0 2 2
2 0 0
2 0 0

样例输出 #1

2

提示

【样例说明】

初始时的图如下所示，每条边上的数字表示这条道路的灰尘度：

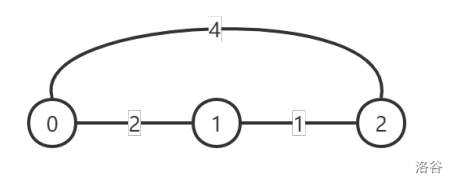
此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

• $d(0,0)=0,d(0,1)=2,d(0,2)=3$；
• $d(1,0)=2,d(1,1)=0,d(1,2)=1$；
• $d(2,0)=3,d(2,1)=1,d(2,2)=0$。

初始时的 $P$ 指标为 $(2+3+1)\times 2=12$，不满足 $P\le Q=10$;

第一天，$0$ 号城市进行道路改善，改善后的图示如下：

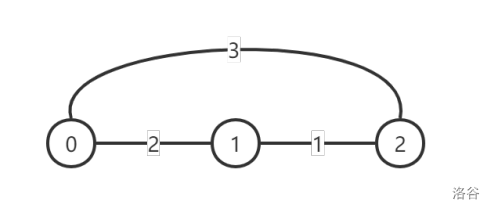
注意到边 $(0,2)$ 的值减小了 $1$，但 $(0,1)$ 并没有减小，因为 $L_{0,1}=2$ ，所以 $(0,1)$ 的值不可以再减小了。此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

• $d(0,0)=0,d(0,1)=2,d(0,2)=3$，
• $d(1,0)=2,d(1,1)=0,d(1,2)=1$，
• $d(2,0)=3,d(2,1)=1,d(2,2)=0$。

此时 $P$ 仍为 $12$。

第二天，1 号城市进行道路改善，改善后的图示如下：

此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

• $d(0,0)=0,d(0,1)=2,d(0,2)=2$，
• $d(1,0)=2,d(1,1)=0,d(1,2)=0$，
• $d(2,0)=2,d(2,1)=0,d(2,2)=0$。

此时的 $P$ 指标为 $(2+2)\times 2=8<Q$，此时已经满足条件。

所以答案是 $2$。

【评测用例规模与约定】

• 对于 $30\%$ 的评测用例，$1\le n\le 10$，$0\le L_{i,j}\le D_{i,j}\le 10$；
• 对于 $60\%$ 的评测用例，$1\le n\le 50$，$0\le L_{i,j}\le D_{i,j}\le 10^5$；
• 对于所有评测用例，$1\le n\le 100$，$0\le L_{i,j}\le D_{i,j}\le 10^5$，$0\le Q\le 2^{31}-1$。

蓝桥杯 2022 国赛 A 组 F 题。

---

---

思路解析

很显然是一道 $Floyd$，可以直接算出多源最短路各点权值。

但是还有个问题：清洁道路减少的灰尘度怎么算？如果按顺序每天更新道路灰尘度，复杂度为 $O(n^3\times k)$，$k$ 为天数，当很显然可能超时，那我们怎么知道最少需要多少天呢？

• 一开始我想用队列来存权值变化的节点，然后更新其他节点值再入队来达到更新所有节点最短路的问题，但是失败了，因为这样就变成了针对队头节点的单源最短路了。

那么应该怎么办？答案是：二分。
我们可以发现：随着天数增加，街道灰尘度单调不增，所以可以用二分来猜答案，每次二分更新街道灰尘度，然后进行 $Floyd$。这样复杂度就是 $O(n^3\cdot logk)$，能过。

---

CODE

#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#define ll long long
#define INF 0x3f3f3f3f using namespace std;typedef pair<int, int> pii;const int N = 110;
int n, Q; // n 是城市的数量，Q 是灰尘度之和的限制
int d[N][N], g[N][N], mini[N][N]; // d[i][j] 表示第 i 个城市和第 j 个城市之间的灰尘度，g[i][j] 表示初始的灰尘度，mini[i][j] 表示最小的灰尘度void floyd(){ // 弗洛伊德算法，用于更新所有城市之间的最短路径（即最小灰尘度）for(int k = 1; k <= n; ++k)for(int i = 1; i <= n; ++i)for(int j = 1; j <= n; ++j)d[i][j] = min(d[i][j], (d[i][k] == INF || d[k][j] == INF) ? INF : d[i][k] + d[k][j]);
}int all(){ // 计算所有城市之间的灰尘度之和int res = 0;for(int i = 1; i <= n; ++i)for(int j = 1; j <= n; ++j)res += d[i][j];return res;
}bool check(int x){ // 检查给定的清洁人数和城市编号是否满足条件int clean = x / n; // 清洁人数int city = x % n; // 城市编号for(int i = 1; i <= n; ++i)for(int j = 1; j <= n; ++j)d[i][j] = g[i][j]; // 恢复初始的灰尘度if(x){        for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){int dif;if(i <= city) dif = clean + 1; // 如果城市编号小于等于给定的编号，那么清洁人数加一else dif = clean;d[i][j] = max(d[i][j] - dif, mini[i][j]); // 更新灰尘度，不能低于最小值d[j][i] = max(d[j][i] - dif, mini[j][i]);}}}floyd(); // 更新最短路径if(all() > Q) return false; // 如果灰尘度之和超过限制，返回 falseelse return true;
}int main(){cin >> n >> Q; // 输入城市数量和限制int dis;for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){scanf("%d", &dis); // 输入初始的灰尘度g[i][j] = dis;}}for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){scanf("%d", &dis); // 输入最小的灰尘度mini[i][j] = dis;}}int l = 0, r = INF, flag = 0, ans = -1;while(l < r){ // 使用二分搜索来找到最小的清洁人数和城市编号int mid = (l + r) >> 1;if(check(mid)) r = mid, ans = mid; // 如果满足条件，那么更新右边界和答案else l = mid + 1; // 否则更新左边界}printf("%d\n", ans); // 输出答案
}

---

给点思考

• 二分这步很妙，看似简单，但是想到不太容易，还是蒟蒻我练少了 >_<
• 每次更新街道的灰尘度，由于是无向图，所以要将双向边都更新。