静态网站建设流程怎么写深圳关键词优化怎么样
看见统计——第四章 统计推断:频率学派
接下来三节的主题是中心极限定理的应用。在不了解随机变量序列 {Xi}\{X_i\}{Xi} 的潜在分布的情况下,对于大样本量,中心极限定理给出了关于样本均值的声明。例如,如果 YYY 是一个 N(0,1)N(0,1)N(0,1) 随机变量,并且{Xi}\{X_i\}{Xi}的独立同分布具有平均值 μμμ 和方差 σ2σ^2σ2,那么
P(X‾−μσ/n∈A)≈P(Y∈A)P(\frac{\overline{X}-\mu}{\sigma /\sqrt{n}}\in A)\approx P(Y\in A) P(σ/nX−μ∈A)≈P(Y∈A)
特别是,如果我们想要一个 YYY 以概率 0.950.950.95 落点的区间,我们可以在网上或书中查找 zzz 表,,对于 N(0,1)N(0,1)N(0,1) 随机变量 YYY ,
P(Y∈(−1.96,1.96))=P(−1.96≤Y≤1.96)=0.95P(Y\in(-1.96,1.96))=P(-1.96\le Y\le 1.96) = 0.95 P(Y∈(−1.96,1.96))=P(−1.96≤Y≤1.96)=0.95
由于X‾−μσ/n\frac{\overline{X}-\mu}{\sigma /\sqrt{n}}σ/nX−μ 接近于 N(0,1)N(0,1)N(0,1) ,这意味着
P(−1.96≤X‾−μσ/n≤1.96)=0.95P(-1.96\le \frac{\overline{X}-\mu}{\sigma /\sqrt{n}}\le 1.96) = 0.95 P(−1.96≤σ/nX−μ≤1.96)=0.95
从上述声明中,我们可以对实验进行陈述,以量化置信度,接受或拒绝假设。
置信区间Confidence Intervals
假设在美国总统选举期间,我们对倾向于支持希拉里而非特朗普的人所占的比例 ppp 感兴趣。我们可以打电话给这个国家的每个人,记录他们支持的人,这种做法显然不现实。相反,我们可以取一堆样本X1,⋯,XnX_1,\cdots,X_nX1,⋯,Xn,其中
Xi={1第i个人更支持希拉里0其它X_i=\begin{cases} 1& 第i个人更支持希拉里\\ 0& 其它 \end{cases} Xi={10第i个人更支持希拉里其它
那么样本均 X‾=1n∑i=1nXi\overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_iX=n1∑i=1nXi 就是我们样本中偏爱希拉里的比例。假设 ppp 是更喜欢希拉里的真实比例( ppp 未知)。注意E(X‾)=pE(\overline{X})=pE(X)=p。然后通过 CLTCLTCLT(中心极限定理),
X‾−μσ/n∼N(0,1)\frac{\overline{X}-\mu}{\sigma /\sqrt{n}} \sim N(0,1) σ/nX−μ∼N(0,1)
由于我们不知道 σσσ 的真实值,我们使用样本方差来估计它,定义如下:
S2≐1n−1∑i=1n(Xi−X‾)2S^2\doteq \frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline{X})^2 S2≐n−11i=1∑n(Xi−X)2
这是 σ2σ^2σ2 的一致估计量,因此当 nnn 很大时,它与真方差 σ2σ^2σ2 相差很大的概率很小。因此,我们可以将表达式中的σσσ 替换为 S=1n−1∑i=1n(Xi−X‾)2S= \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline{X})^2}S=n−11∑i=1n(Xi−X)2。由于X‾−μS/n\frac{\overline{X}-\mu}{S /\sqrt{n}}S/nX−μ 接近于 N(0,1)N(0,1)N(0,1) ,这意味着
P(−1.96≤X‾−μS/n≤1.96)=0.95P(-1.96\le \frac{\overline{X}-\mu}{S /\sqrt{n}}\le 1.96) = 0.95 P(−1.96≤S/nX−μ≤1.96)=0.95
重新排列 ppp 的表达式,我们有
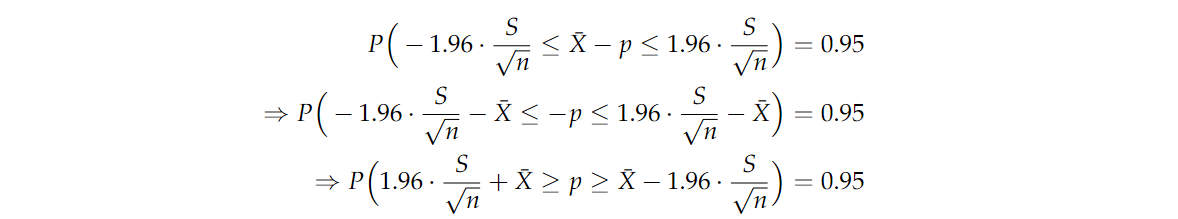
即使我们不知道 ppp 的真实值,我们可以从上面的表达式得出结论, ppp 有0.95的概率在如下区间中:
(X‾−1.96⋅Sn,X‾+1.96⋅Sn)(\overline{X}-1.96 \cdot \frac{S}{\sqrt{n}},\overline{X}+1.96 \cdot \frac{S}{\sqrt{n}}) (X−1.96⋅nS,X+1.96⋅nS)
这被称为参数 ppp 的95%的置信度区间。此近似适用于较大的 nnn 值,通常要确保 n>30n>30n>30 。可视化如下:

假设检验Hypothesis Testing
让我们回到2016年总统选举中决定选民偏好的例子。假设我们怀疑支持希拉里的选民比例大于1/21/21/2 ,并且我们从美国人口中抽取了标记为 {Xi}in=1\{X_i\}^n_i=1{Xi}in=1的样本。基于这些样本,我们能支持或否定希拉里更受欢迎的假设吗?我们对我们的结论有多大的信心?假设检验是帮助回答这些问题的完美工具。
构建一个测试
本文中的假设是关于感兴趣的参数的声明。在总统选举的例子中,感兴趣的参数是 ppp ,即支持希拉里的人所占的比。那么一个假设可能是 p>0.5p>0.5p>0.5 ,即超过一半的人支持希拉里。
假设检验有四个主要组成部分。
-
备择假设alternative hypothesis,表示为HaH_aHa ,是一个我们想要支持的主张。在前面的例子中,备择假设为 p>0.5p>0.5p>0.5 。
-
零假设null hypothesis,记为 H0H_0H0,与备择假设相反。在这种情况下,零假设是 p≤0.5p≤0.5p≤0.5 ,即只有不到一半的人支持希拉里。
-
检验统计量test statistic,是样本观测值的函数。基于检验统计量,我们将接受或拒绝零假设。在前面的例子中,检验统计量是样本均值 X‾\overline{X}X 。样本均值通常是许多假设检验的检验统计量。
-
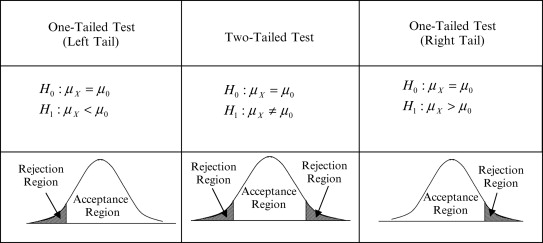
拒绝域rejection region是样本空间 ΩΩΩ 的子集,它决定是否拒绝零假设。如果检验统计量落在拒绝域,那么我们拒绝原假设。否则,我们接受。在总统选举的例子中,拒绝区域为
RR:{(x1,x2,...,xn):X‾>k}RR:\{(x_1,x_2,...,x_n):\overline{X}>k\} RR:{(x1,x2,...,xn):X>k}
这种表示法意味着如果 X‾\overline{X}X 落在区间 (k,∞)(k,∞)(k,∞),我们将拒绝,其中 kkk 是我们必须确定的某个数字。kkk由Type I error决定,它在下一节中定义。一旦计算出 kkk ,我们根据检验统计量的值拒绝或接受零假设,检验完成。
错误类型
在假设检验中有两种基本类型的错误。它们分别表示为 III 型和 IIIIII 型错误。
🔥 定义 :当 H0H_0H0 实际上为真,我们却拒绝它时,就犯了 III 型错误。Type I error的概率通常记为 ααα。
换句话说,ααα 是假阳性的概率。
🔥 定义 :当 H0H_0H0 实际上为假,我们却接受它时,就犯了 IIIIII 型错误。Type II error的概率通常记为 βββ。
换句话说, βββ 是假阴性的概率。
在假设检验的背景下, ααα 将决定拒绝域。如果我们将假阳性的概率限制在小于0.05,那么我们有
P(X‾∈RR∣H0)≤0.05P(\overline{X}\in RR|H_0)\le 0.05 P(X∈RR∣H0)≤0.05
即假设 H0H_0H0 为真,我们的检验统计量落在拒绝域(意味着我们拒绝 H0H_0H0 ),概率为0.05。继续我们的总统选举的例子,拒绝域的形式是 X‾>k\overline{X} > kX>k,零假设是 p≤0.5p≤0.5p≤0.5。我们上面的表达式就变成了
P(X‾>k∣p≤5)≤0.05P(\overline{X}>k|p\le 5)\le 0.05 P(X>k∣p≤5)≤0.05
如果 n>30n>30n>30 ,那我们可以应用中心极限定理
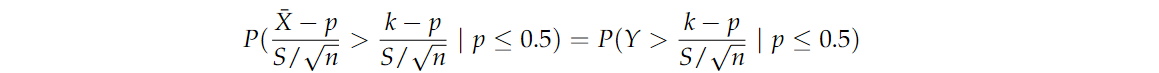
其中 YYY 是 N(0,1)N(0,1)N(0,1) 的随机变量。由于 p≤0.5p≤0.5p≤0.5 意味着 k−pS/n≥k−0.5S/n\frac{k-p}{S/\sqrt{n}} \ge \frac{k-0.5}{S/\sqrt{n}}S/nk−p≥S/nk−0.5,我们也必须有
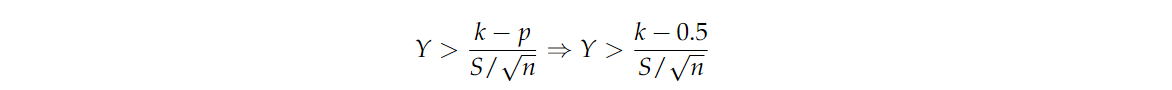
因此

因此,如果我们将不等式右侧的概率限定为0.05,那么我们也将不等式左侧的概率(I型误差 ααα )限定为0.05。由于 YYY 是 N(0,1)N(0,1)N(0,1) 的随机变量,我们可以查 zzz 表,找到 z0.05=−1.64z_{0.05} =−1.64z0.05=−1.64,因此
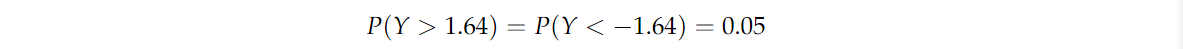
设k−0.5S/n=1.64\frac{k-0.5}{S/\sqrt{n}}=1.64S/nk−0.5=1.64,我们可以求解 kkk 来确定拒绝域:
k=0.5+1.64⋅Snk=0.5+1.64\cdot \frac{S}{\sqrt{n}} k=0.5+1.64⋅nS
由于我们的拒绝域形式为 X‾>k\overline{X} > kX>k,我们只需检查 X‾>0.5+1.64⋅Sn\overline{X} > 0.5+1.64\cdot \frac{S}{\sqrt{n}}X>0.5+1.64⋅nS。如果这是真的,那么我们拒绝零假设,并得出结论,超过一半的人口支持希拉里。因为我们设 α=0.05α = 0.05α=0.05 ,所以我们有 1−α=0.951−α = 0.951−α=0.95 的把握相信我们的结论是正确的。
在上面的例子中,我们通过为 ppp 代入0.5来确定拒绝域,即使零假设为 p≤0.5p≤0.5p≤0.5 。这就好像我们的零假设是H0:p=0.5H_0: p = 0.5H0:p=0.5,而不是H0:p≤0.5H_0: p≤0.5H0:p≤0.5。一般来说,当我们确定拒绝域时,可以简化 H0H_0H0 ,并假设边界情况(在这种情况下 p=0.5p = 0.5p=0.5)。
p-Values
正如我们在上一节中看到的,选定的 ααα 确定了拒绝域,因此假阳性的概率小于 ααα 。现在假设我们观察一些检验统计数据,比如说,支持希拉里的选民 X‾\overline{X}X 的样本比例。然后,我们提出以下问题。给定 X‾\overline{X}X,使我们仍然拒绝零假设的 ααα 的最小值是多少?这将引出以下定义。
p=min{α∈(0,1):Reject H0using an α level test}p =\min\{\alpha \in(0,1):\text{Reject}\ H_0\ \text{using an α level test}\} p=min{α∈(0,1):Reject H0 using an α level test}
ppp 值即我们仍然拒绝零假设的 ααα 的最小值。
下面我们通过一个例子来说明。
🍌 假设我们对 nnn 个人进行抽样,问他们更喜欢哪个候选人。就像我们之前做的那样,我们可以将每个人表示为一个指标函数,
Xi={1第i个人更支持希拉里0其它X_i=\begin{cases} 1& 第i个人更支持希拉里\\ 0& 其它 \end{cases} Xi={10第i个人更支持希拉里其它
那么 X‾\overline{X}X 是样本中倾向于希拉里的比例。在取了 nnn 个样本后,假设我们观察到 X‾=0.7\overline{X}=0.7X=0.7 。如果我们要建立一个假设检验,我们的假设,检验统计量和拒绝域将是
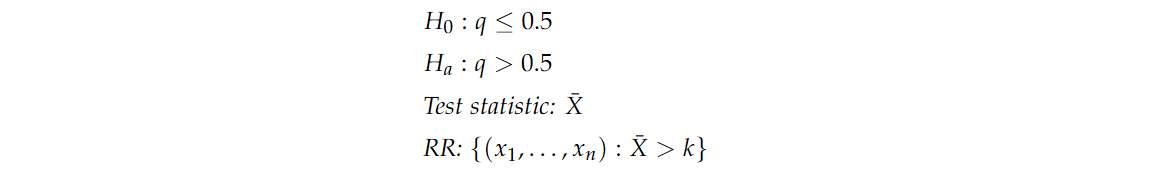
其中 qqq 是整个美国人口中支持希拉里的真实比例。使用直观的定义,ppp 值是我们观察到比 0.70.70.7 更极端的概率。由于零假设是 q≤0.5q≤0.5q≤0.5 ,在这种情况下,"更极端” 意味着 “大于0.7”。因此,ppp 值是指在给定一个新的样本时,我们观察到新 X‾\overline{X}X 大于0.7的概率,假设无效,即 q≤0.5q≤0.5q≤0.5。 X‾\overline{X}X 归一化有
P(X‾>0.7∣H0)=P(X‾−0.5S/n>0.7−0.5S/n)≈P(Y>0.7−0.5S/n)≐pP( \overline{X}>0.7|H_0 )=P(\frac{\overline{X}-0.5}{S/\sqrt{n}}>\frac{0.7-0.5}{S/\sqrt{n}})\approx P(Y>\frac{0.7-0.5}{S/\sqrt{n}})\doteq p P(X>0.7∣H0)=P(S/nX−0.5>S/n0.7−0.5)≈P(Y>S/n0.7−0.5)≐p
其中 Y∼N(0,1)Y\sim N(0,1)Y∼N(0,1)。然后,我们将计算值 zp≐0.7−0.5S/nz_p\doteq \frac{0.7-0.5}{S/\sqrt{n}}zp≐S/n0.7−0.5。然后,我们将查找 zzz 表并找到与 zpz_pzp 对应的概率,记为 ppp (就是我们的 ppp 值)。
Bootstrap
Bootstrap又称自展法、自举法、自助法、靴带法 , 是统计学习中一种重采样(Resampling)技术,用来估计标准误差、置信区间和偏差
Bootstrap是现代统计学较为流行的一种统计方法,在小样本时效果很好。机器学习中的Bagging,AdaBoost等方法其实都蕴含了Boostrap的思想,在集成学习的范畴里 Bootstrap直接派生出了Bagging模型.
子样本之于样本,可以类比样本之于总体

参考
- https://github.com/seeingtheory/Seeing-Theory
- 统计学中的Bootstrap方法(Bootstrap抽样)
