学习目标：

如果我要学习函数的单调性和曲线的凹凸性，我会采取以下几个步骤：

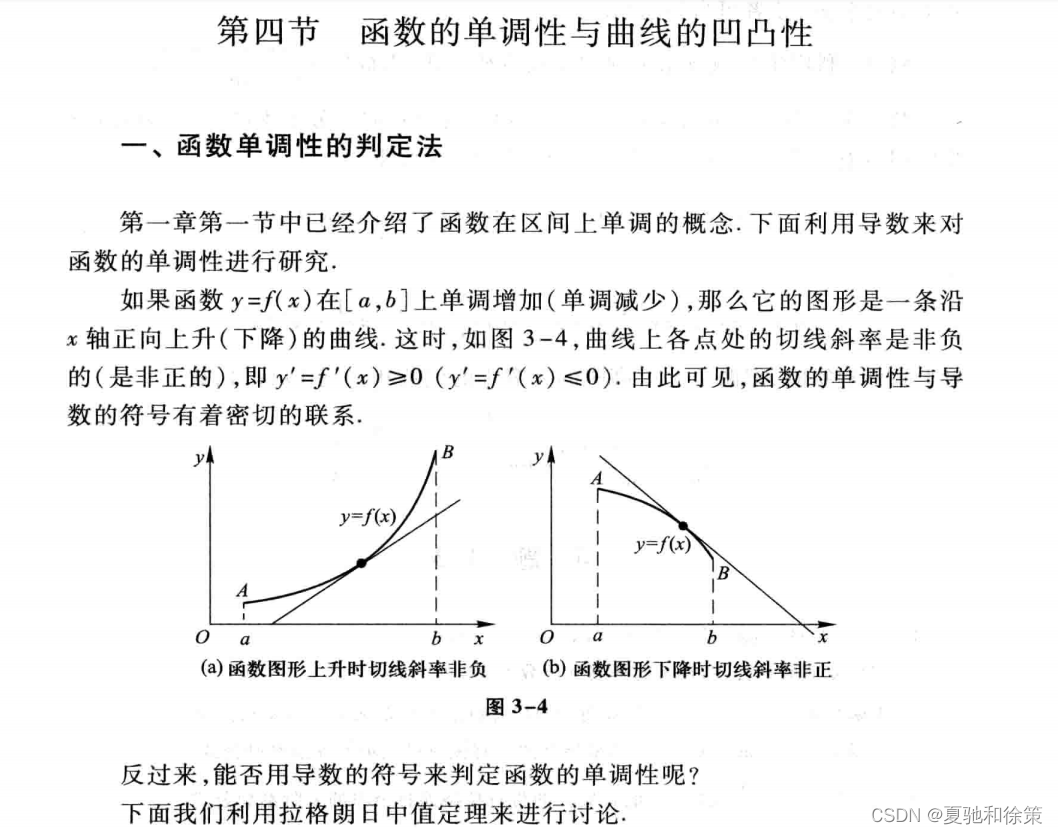
1. 理解概念和定义：首先，我会学习单调性和凹凸性的定义和概念。单调性是指函数的增减性质，可以分为单调递增和单调递减；凹凸性是指函数的弯曲程度，可以分为凹和凸。我会理解这些概念的意义和特点，以及如何通过图像来判断函数的单调性和凹凸性。

2. 掌握判断方法：其次，我会掌握判断函数单调性和凹凸性的方法。例如，函数的导数可以用来判断函数的单调性和凹凸性，对于单峰函数或双峰函数，还可以通过二阶导数的符号来判断其凹凸性。我会学习这些方法的原理和应用，通过练习来提高自己的判断能力。

3. 熟练运用：接着，我会通过练习来熟练运用判断函数单调性和凹凸性的方法。我会选取不同类型的函数，例如多项式函数、三角函数、指数函数等，来练习如何判断它们的单调性和凹凸性。我会注重练习，通过不断地尝试和纠错，提高自己的判断水平和准确性。

4. 应用于问题：最后，我会应用所学的知识来解决实际问题。例如，在最优化问题中，函数的单调性和凹凸性可以用来确定函数的极值点和拐点，从而帮助我们找到最优解。我会通过实际问题的练习来应用所学的知识，加深自己对单调性和凹凸性的理解和掌握。

 

 

 

 

 

 

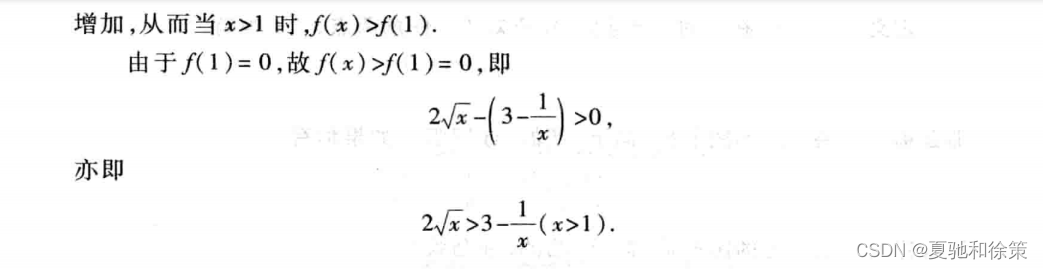 我的理解：

函数的单调性是指函数的增减规律。在数学中，通常分为严格单调递增、严格单调递减、非严格单调递增和非严格单调递减四种情况。下面是函数单调性的判断方法：

1. 导数法：如果函数在定义域内的导数大于 0，则函数在该区间内严格单调递增；如果导数小于 0，则函数在该区间内严格单调递减。如果导数等于 0，则需要进一步分析。

2. 二阶导数法：如果函数在定义域内的二阶导数大于 0，则函数在该区间内非严格单调递增；如果二阶导数小于 0，则函数在该区间内非严格单调递减。如果二阶导数等于 0，则需要进一步分析。

3. 利用单调性的定义：如果函数在一个区间内单调递增，那么在这个区间内任意两个点的函数值都有 f(x1) < f(x2) 成立。反之，如果函数在一个区间内单调递减，那么在这个区间内任意两个点的函数值都有 f(x1) > f(x2) 成立。

4. 图像法：根据函数图像的走势，可以判断函数的单调性。如果函数图像在某个区间内向上倾斜，则函数在该区间内单调递增；如果函数图像在某个区间内向下倾斜，则函数在该区间内单调递减。注意，这种方法只适用于简单的函数图像。

以上是函数单调性的判断方法，根据实际情况和题目要求可以灵活选择。需要注意的是，有些函数并不具备单调性，这时需要特殊分析。

 

 

 

 

 我的理解：

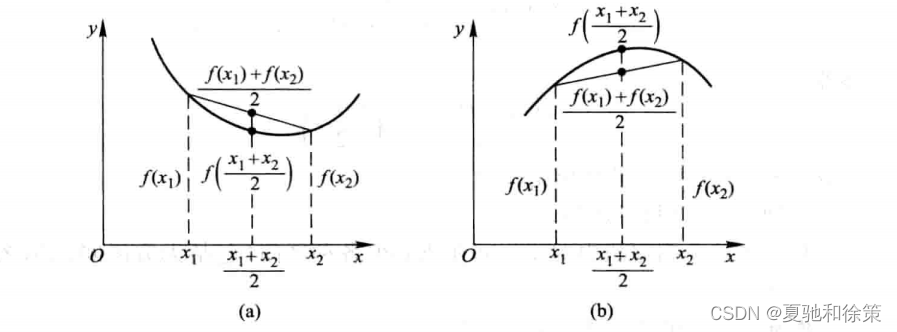
函数的凹凸性是指函数图像的弯曲程度，具体地说，如果函数图像在一个区间内向上弯曲，那么该区间内函数具有凹性；如果函数图像在一个区间内向下弯曲，那么该区间内函数具有凸性。函数的凹凸性分为严格凹函数、严格凸函数、非严格凹函数和非严格凸函数四种情况。

拐点是指函数图像由凹性向凸性或者由凸性向凹性转变的点，即函数的凹凸性发生改变的点。拐点处的二阶导数为 0，但不一定是拐点，还需要根据一阶导数的正负情况来判断。

下面是函数凹凸性和拐点的判断方法：

1. 导数法：如果函数在定义域内的二阶导数大于 0，则函数在该区间内具有凸性；如果二阶导数小于 0，则函数在该区间内具有凹性。如果二阶导数等于 0，则需要进一步判断一阶导数的正负情况，如果一阶导数在拐点处发生正向变化，则该点为拐点，且函数从凹性转变为凸性；如果一阶导数在拐点处发生负向变化，则该点为拐点，且函数从凸性转变为凹性。

2. 利用函数凹凸性的定义：如果函数在一个区间内具有凸性，那么在该区间内任意两个点的函数值都有 f((x1+x2)/2) < (f(x1) + f(x2))/2 成立。如果函数在一个区间内具有凹性，那么在该区间内任意两个点的函数值都有 f((x1+x2)/2) > (f(x1) + f(x2))/2 成立。如果在某个点上两个式子都成立，那么该点就是拐点。

3. 图像法：通过观察函数图像，可以直观地判断函数的凹凸性和拐点。在函数图像上，凹性表现为图像向上弯曲，凸性表现为图像向下弯曲，拐点表现为图像从向上弯曲转变为向下弯曲，或者从向下弯曲转变为向上弯曲的位置。

以上是函数凹凸性和拐点的判断方法，需要根据实际情况和题目要求进行灵活运用。

 总结

 

函数的单调性和曲线的凹凸性是微积分中重要的概念之一，它们与函数的导数、二阶导数等密切相关。下面是它们的重点、难点和易错点：

1. 函数的单调性

重点：定义和判断方法。可以利用导数的符号判断函数的单调性。当导数$f'(x)$在定义域上恒大于零时，函数递增；当导数f'(x)在定义域上恒小于零时，函数递减。

难点：拐点。拐点处函数单调性可能发生变化，需要根据二阶导数f''(x)的符号进行判断。

易错点：区间判断。判断函数的单调性时要注意定义域上是否连续，以及是否存在间断点等特殊情况。此外，要注意区间的开闭性和函数值的取值范围等细节。

1. 曲线的凹凸性

重点：定义和判断方法。可以利用二阶导数f'(x)的符号判断曲线的凹凸性。

难点：拐点。拐点处曲线的凹凸性可能发生变化，需要根据三阶导数$f'''(x)$的符号进行判断。

易错点：凸区间与凹区间。在某些情况下，曲线的凸凹性可能在同一个区间内交替出现。此外，要注意区间的开闭性和函数值的取值范围等细节。