java开发网站怎么做网址seo查询

Patch & Window

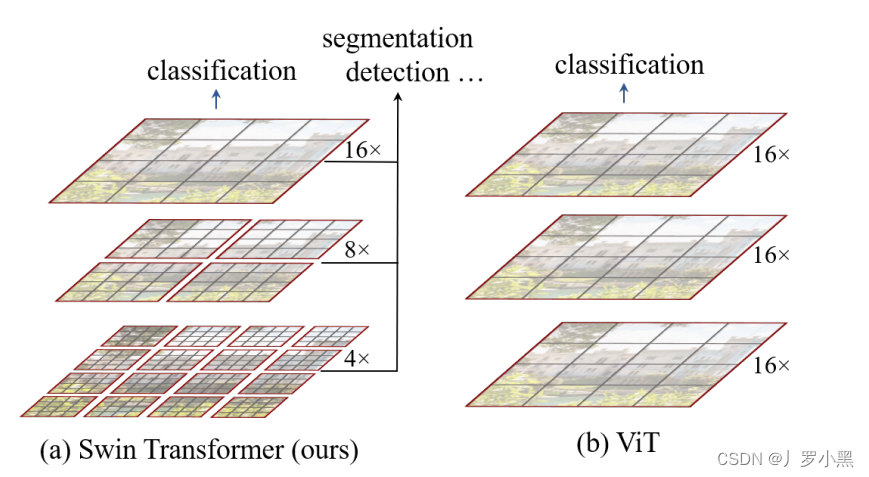
• 在Swin Transformer中，不同层级的窗口内部的补丁数量是固定的，补丁内部的像素数量也是固定的，如上图的红色框就是不同的窗口（Window），窗口内部的灰色框就是补丁（Patch）
• 如果输入图像的宽W、高H，增加到原来的两倍，那么输入图像的总面积（总像素数量）就增加到原来的四倍（2H * 2W = 4HW）
• 在ViT中，由于窗口是固定的，且就是整个输入图片，所以当我们将输入图片分割成很多个尺寸为16 * 16 的patch时，如果输入图像的总面积增加到原来的四倍，那么patch的数量也会变成原来的四倍，那么计算复杂度$O(N^2\cdot d)$，就变成了$O((4N{)}^2\cdot d)=O(16N^2\cdot d)$，其中d是每个patch的维度，N是patch的数量。因此，对于ViT来说，计算复杂度是跟图像增加的大小成平方关系
• 在Swin Transformer中，由于窗口不是固定的，但是窗口内部的补丁数量是固定的，补丁的尺寸也是固定的，所以当我们将输入图片的总面积增加到原来的四倍，那么只有窗口的数量增加到原来的四倍，那么计算复杂度$O(M^2\cdot N\cdot d)$，就变成了$O(M^2\cdot 4N\cdot d)$，其中M是每个窗口内补丁的数量，N是窗口的数量，d是每个补丁patch的维度。（虽然每个patch的维度都不一样，这里先不管了）

Swin Transformer

Swin Transformer 提出ViT具有两个缺点：
1. 没有多尺度特征 ，不能生成多尺度的特征图传给FPN (检测) \ U-Net (分割)，从而对于不同大小的物体都能进行良好感知
3. 全局计算自注意力浪费资源，并且计算复杂度跟图像增加的大小成平方关系
对于以上缺点，Swin Transformer给出了以下的解决方法：

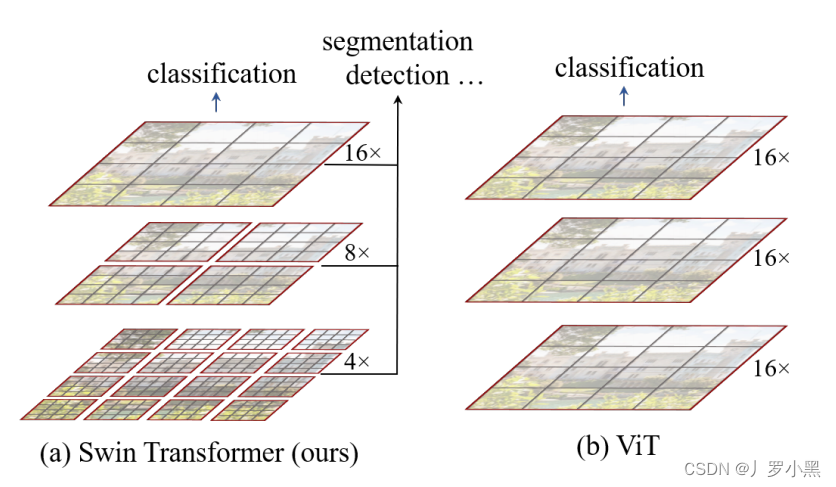
• 不同于ViT—在整张输入图片上进行自注意力计算。Swin Transformer是在窗口内进行自注意力计算的，同时这个窗口又是包含固定数量的patch，每个patch的尺寸也是固定的。由于在图像领域中，同一个物体的不同部位、或语义相似的不同物体大概率会出现在相邻的地方，所以没必要像ViT那样–对整张图进行自注意力操作，其实可以借鉴CNN卷积的局部性的归纳偏置，在一个小的局部窗口内进行自注意力计算，也是差不多够用的。所以Swin Transformer使用了尺寸不一的窗口来避免序列长度过大，从而节约计算资源。
• 不同于ViT— 在每个Transformer Encoder Block上都是做相同尺寸的自注意力操作，得到的也是相同尺寸的特征。Swin Transformer在不同尺寸的窗口内做自注意力操作，从而得到不同尺寸的特征图，也就是多尺度的特征图。
• 在Swin Transformer中，这叫做patch merging。这跟CNN的池化操作很类似，CNN通过池化Pooling，来增大每一个卷积核能看到的感受野，从而使每次池化后的卷积核能够抓住不同尺寸的物体。
  
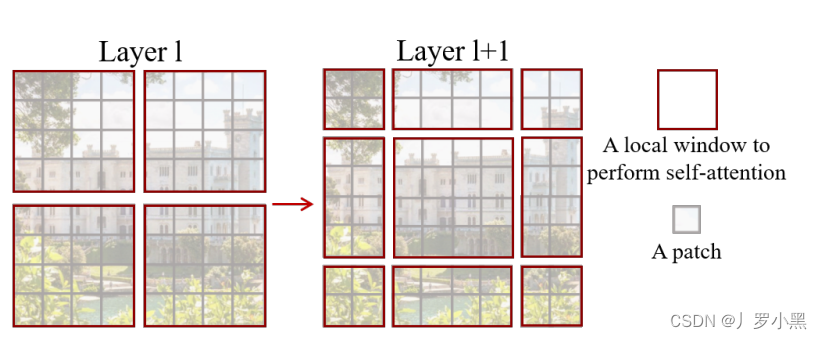
• 在Swin Transformer中，灰色的格子叫patch是最小的计算单元（尺寸为4 * 4），红色的格子叫window是中等的计算单元，最小的窗口里有7 * 7个patch，通过将整张图分成不同的窗口，只计算窗口内的自注意力，可以极大程度的减小序列长度，减小计算复杂度。
• shifted window是指：先将左侧图中的分割线往右下移动两个patch，然后将左上角变大后的窗口重新按中心分割成四个窗口，再将分割线往左上移动两个patch，就变成右图的样子。
• shifted window 和 patch merging的好处如下：
  1. 当我们进行注意力计算的时候，只在Swin Transformer的局部窗口内进行局部自注意力计算，相比ViT的全局窗口来说，可以减少序列长度，节省内存，加快计算。
  2. 因为自注意力都是只在窗口内进行，所以如果不进行shift，那么某个窗口内的patch就永远无法注意到其他窗口内patch的信息，这就违背了Transformer的初衷—更好的理解上下文，掌握全局信息。但是经过shift之后，比如中间的窗口，就是由之前四个窗口的patch组成的，也就表示中间窗口进行自注意力计算后，可以关注到其他窗口的信息，窗口和窗口之间可以进行交互（Cross-Window Connection）
  3. 再加上之前的patch merging，那么在不断合并的时候，每个patch可以注意到很多其他窗口的patch信息，即每个patch的感受野会不断增大
  4. 因此虽然我们计算的是每个窗口内的局部自注意力，但是实际上它近似等于一个全局的自注意力。

池化

• 如果使用卷积核大小为（1 * 2）具体为 [1 , -1]，由于卷积操作对位置很敏感，所以对最左侧的输入进行卷积之后，得到的结果只有一列是1，即边缘会检测不准，如果当图片发生微小改变后，边缘经过卷积都会发生变化。所以卷积对于位置的敏感性不是一个很好的事。因此最好能具有一定程度的平移不变性，即当图片发生微小的改变，卷积结果不会发生改变。
  
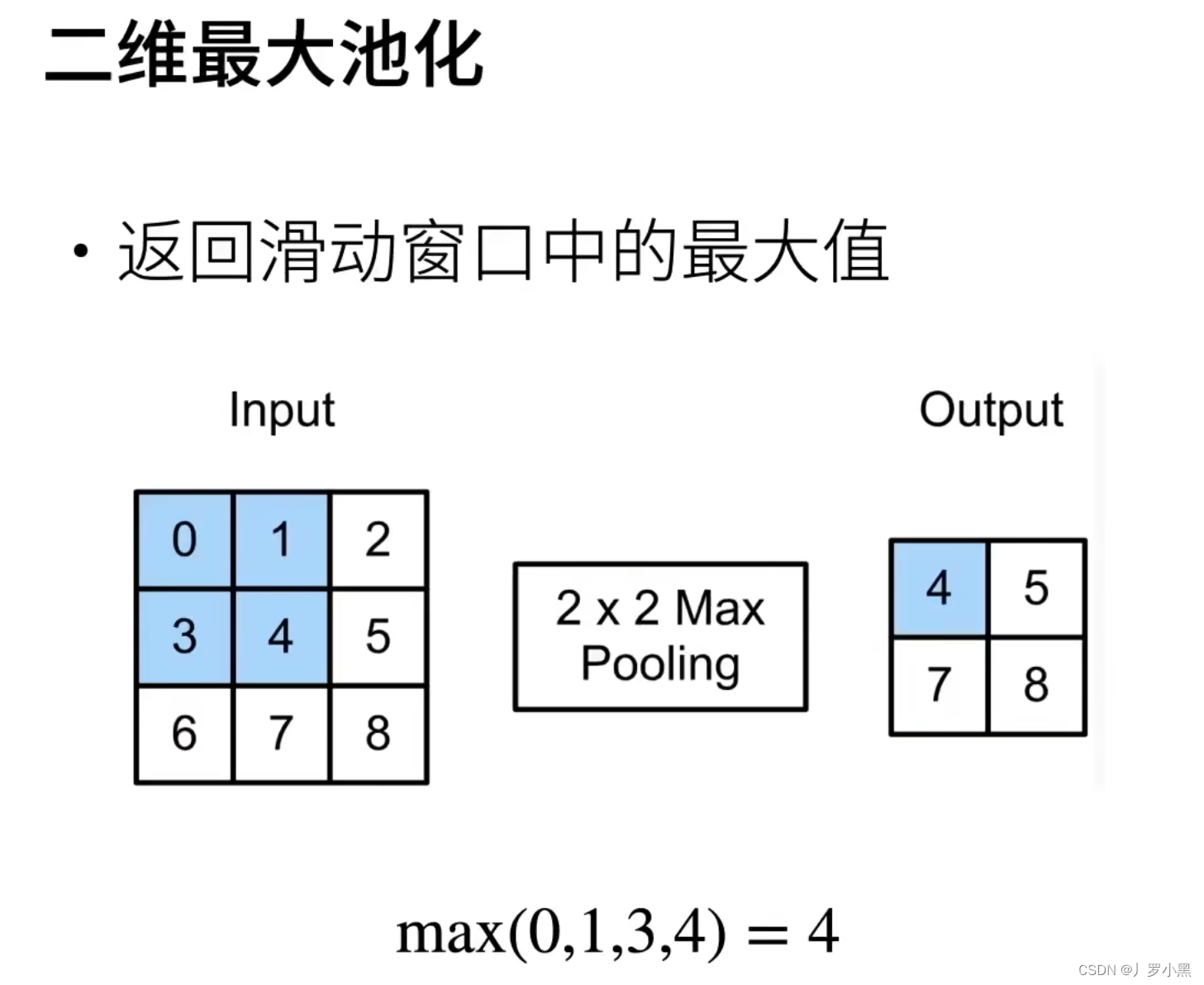
• 所以往往在卷积之后加入池化操作，以上是二维最大池化的示意过程
  
• 通过二维最大池化的结果可以看出，池化的操作近似于模糊化，在卷积输出的值附近出现多次同样的值。
• 池化层和卷积层类似，都有填充和步幅
• 但是池化层没有可学习的参数，直接从输入中选取值了
• 池化层的输出通道数等于输入通道数，即在每个输入通道应用池化层来获得相对应的输出通道。（由于卷积层可以改变通道，而池化层往往是跟在卷积层后面，所以池化层就不需要改变通道数了）