广州番禺疫情风险等级小红书seo排名

一、简介

1.1 什么是动态规划？

在说明动态规划前，我们先来了解一个小场景：

A: "1+1+1+1+1+1+1+1"A: "上面等式的值是多少？"
B: "（计算...）" "8!"A: "在上面等式的左边写上 '1+'，此时等式的值为多少？"
B: "（立刻回答）" "9!"
A: "你这次怎么这么快就知道答案了"
B: "只要在8的基础上加1就行了"

由上面的小故事可知，动态规划 就是 通过记住历史的求解结果来节省时间 。

1.2 动态规划的两种形式

示例：斐波那契数列，又称黄金分割数列，其数值为：1、1、2、3、5、8、13、21、34，递推公式为：
$$F(0)=1,F(1)=1,F(n)=F(n-1)+F(n-2),n>2,n\in N^{\ast }$$
这个算法用递归来实现非常简单，代码如下：

public int fib(int n) {if (n < 2) {return 1;}return fib(n - 1) + fib(n - 2);
}

先来分析一下递归算法的执行流程，假如输入 6，那么执行的递归树如下：

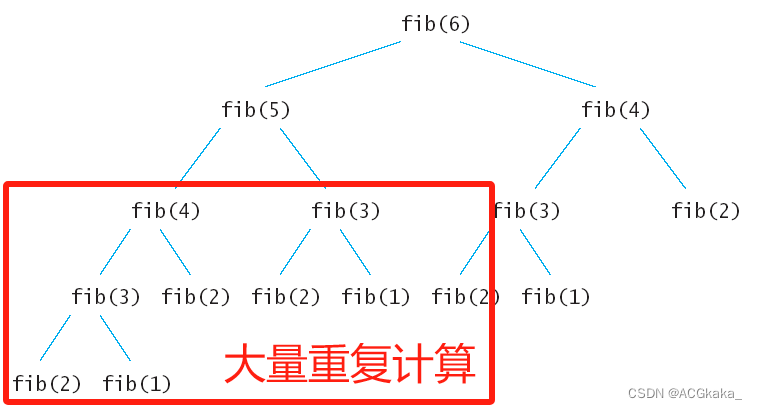
我们可以发现：

• 上面的递归树中，每一个结点都会执行一次；
• 很多结点被重复执行。

为了避免这种情况，我们可以把执行过的结点值保存下来，后面用到直接查表，这样可以节省大量时间。

下面看下保存历史记录的两种形式：自顶向下的备忘录法、自底向上的动态规划。

1）自顶向下的备忘录法（记忆化搜索法）

备忘录法，也叫记忆化搜索法，是比较好理解的：

• 创建了一个 n+1 大小的数组来保存求出斐波那契数列中的每一个值；
• 在递归的时候，如果发现之前已经算过了就不再计算；
• 如果之前没有计算，则计算后放入历史记录中。

public static void main(String[] args) {int n = 6;// 声明数组，用于记录历史，初始化为-1int[] his = new int[n + 1];Arrays.fill(his, -1);System.out.println(fib(n, his));
}public static int fib(int n, int[] his) {if (n < 2) {return 1;}// 读取历史if (his[n] != -1) {return his[n];}int result = fib(n - 1, his) + fib(n - 2, his);// 记录历史his[n] = result;return result;
}

2）自底向上的动态规划

备忘录法还是利用了递归，不管怎样，当计算 fib(6) 的时候还是要去先计算出 fib(1) ~ fib(5)，那么为何不先计算出 f(1) ~ f(5) 呢？这就是动态规划的核心：先计算子问题，再由子问题计算父问题。

public static int fib(int n) {int[] arr = new int[n + 1];arr[0] = 1;arr[1] = 1;for (int i = 2; i <= n; i++) {arr[i] = arr[i - 2] + arr[i - 1];}return arr[n];
}

自底向上的动态规划方法也是利用数组保存了计算的值，为后面的计算使用。

内存空间优化：

我们观察上面的代码会发现：参与循环的只有 fib(i)、fib(i-1)、fib(i-2) 项，因此该方法的空间可以进一步的压缩如下：

public static int fib(int n) {int num_i = 0;int num_i_1 = 1;int num_i_2 = 1;for (int i = 2; i <= n; i++) {num_i = num_i_2 + num_i_1;num_i_2 = num_i_1;num_i_1 = num_i;}return num_i;
}

3）两种方法对比

• 一般来说，由于备忘录的动态规划形式使用了递归，递归的时候会产生额外的开销，所以不推荐。
• 相比之下，使用自底向上的动态规划方法要好些，也更容易理解。

1.3 动态规划的 3 大步骤

动态规划，无非就是利用 历史记录，来避免我们的重复计算。这些历史记录的存储，一般使用 一维数组 或 二维数组 来保存。

第一步：定义数组元素的含义

• 上面说了，我们用一个数组来保存历史数据，假设用一维数组 dp[] 来保存。这个时候有一个非常重要的点：如何规定数组元素的含义？ 即 dp[i] 代表什么意思？

第二步：找出数组元素之间的关系

• 动态规划类似于我们高中学习的 数学归纳法。当我们要计算 d[i] 时，可以利用 dp[i-1]、dp[i-2] … dp[1] 来推导证明。

第三步：找出初始值

• 学过 数学归纳法 的都知道，虽然知道了数组元素之间的关系式后，可以通过 dp[i-1] 和 dp[i-2] 来计算 dp[i]，但是我们首先至少要知道 dp[0] 和 dp[1] 才能推导后面的值。dp[0] 和 dp[1] 就是所谓的初始值。

二、小试牛刀：钢条切割

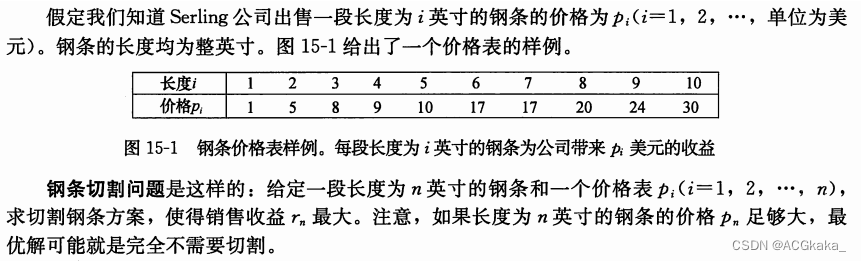
2.1 题目描述

2.2 题目解析

1）第一步：定义数组元素的含义

由题目可知：

• p[] 是价格数组，长度为 i 英寸的钢条价格为 p[i]；
• r[] 是最大收益数组，长度为 i 英寸的钢条可以获得的最大收益为 r[i]；
• 钢条的价格不确定，可能切割的收益更高，也可能不切割的收益更高。

通过解析可知，数组元素含义： 长度为 i 英寸的钢条可以获得的最大收益为 r[i]。

注意： 这里的 收益是指价格的总和，比如：2 英寸的钢条切割后收益为：1+1=2，相比之下不切割的 5 收益更高。

2）第二步：找出数组元素之间的关系

假如我们要对长度为 4 英寸的钢条进行切割，所有切割方案如下：

由图可见，我们将 r[4] 的计算转换成了 r[1]~ r[3] 的计算。
$$r_4=max(r_1+r_3,r_1+r_1+r_2,r_2+r_2,p_4);$$
以此类推，可以继续转换 r[3]：

由图可见，我们继续将 r[3] 的计算转换成了 r[1]~r[2] 的计算。
$$r_3=max(r_1+r_2,r_1+r_1+r_1,p_3)$$
以此类推，可以继续转换 r[2]：

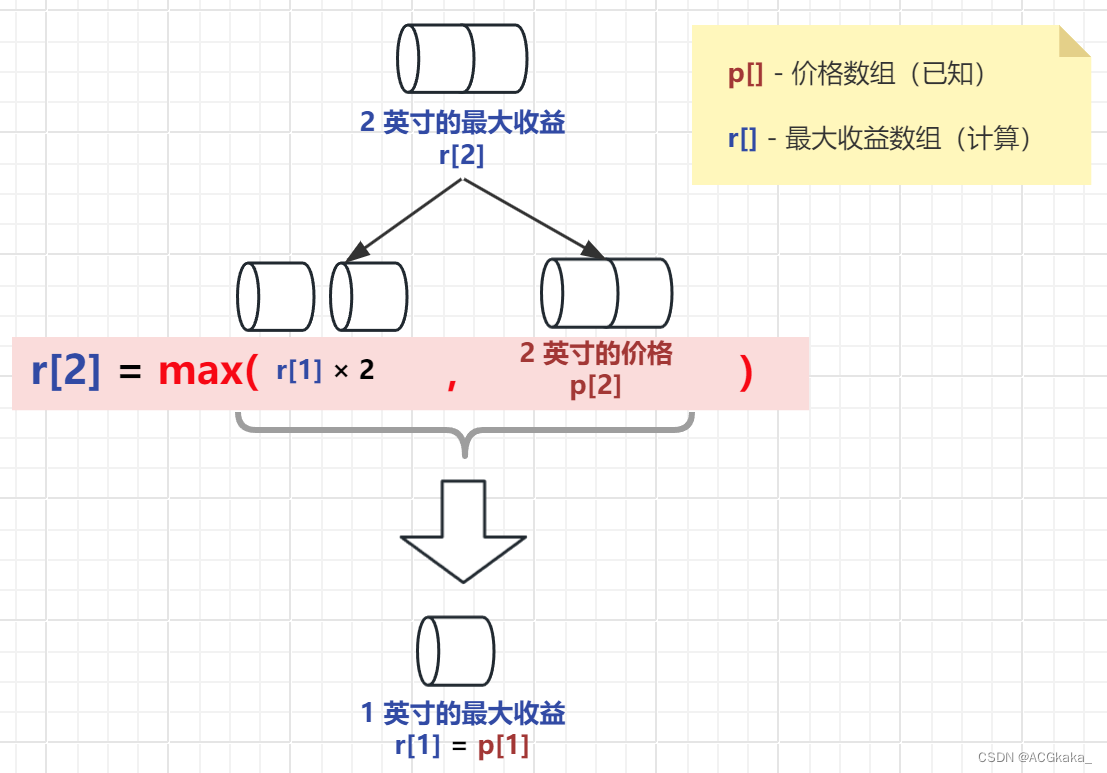
由于 1 英寸的钢条无法切割，所以 r[1]=p[1]。
$$r_2=max(r_1+r_1,p_2)$$
由于 r[2] 中包含了 r[1] + r[1]，那么 r[3] 中的：
$$max(r_1+r_2,r_1+r_1+r_1)=max(r_1+r_2)$$
由于 r[3] 中包含了 r[1] + r[2]，那么 r[4] 中的：
$$max(r_1+r_3,r_1+r_1+r_2)=max(r_1+r_3)$$
所以整理 r[1]、r[2]、r[3]、r[4] 为：
$$r_1=p_1$$

$$r_2=max(r_1+r_1,p_2)$$

$$r_3=max(r_1+r_2,p_3)$$

$$r_4=max(r_1+r_3,r_2+r_2,p_4)$$

根据公式进行递推， r[n] 为：
$$r_n=max(r_1+r_{n-1},r_2+r_{n-2},...,r_{n/2}+r_{n-n/2},p_n)$$

3）第三步：找出初始值

其实初始值我们在第二步已经找出来了：

• r[1]=p[1]=1
• r[2]=max(r[1]+r[1],p[2])=5

2.3 最优子结构

通过该题我们注意到，为了求规模为n的原问题，我们 先求解形式完全一样，但规模更小的子问题。当完成首次 切割后，我们 将两段钢条看成两个独立的钢条切割问题实例。我们 通过组合两个相关子问题的最优解，并在所有可能的两段切割方案中选取组合收益最大者，构成原问题的最优解。

我们称 钢条切割问题 满足 最优子结构 性质：问题的最优解由相关子问题的最优解组合而成，而这些子问题可以独立求解。

2.4 代码实现

1）递归版本

递归很好理解，思路和回溯法是一样的，遍历所有解空间。但这里和上面斐波那契数列的不同之处在于：这里在每一层上都进行了一次最优解的选择，q=Math.max(q, p[i]+cut(n-i)); 这段代码就是选择最优解。

final static int[] p = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};public static int cut(int n) {if (n == 0) {return 0;}int max = Integer.MIN_VALUE;for (int i = 1; i <= n; i++) {max = Math.max(max, p[i - 1] + cut(n - i));}return max;
}

2）备忘录版本

备忘录方法无非是在递归的时候记录下已经调用过的子函数的值。钢条切割问题的经典之处在于自底向上的动态规划问题的处理，理解了这个也就理解了动态规划的精髓。

public static int cutByHis(int n) {int[] p = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};int[] r = new int[n + 1];for (int i = 0; i <= n; i++) {r[i] = -1;}return cut(p, n, r);
}public static int cut(int[] p, int n, int[] r) {int q = -1;if (r[n] >= 0)return r[n];if (n == 0)q = 0;else {for (int i = 1; i <= n; i++)q = Math.max(q, cut(p, n - i, r) + p[i - 1]);}r[n] = q;return q;
}

3）自底向上的动态规划

自底向上的动态规划问题中最重要的是要理解在子循环遍历中的 i 变量，相当于上面两个方法中的 n 变量，i-j 主要用于获取历史计算过的问题值。

final static int[] p = {1, 5, 8, 9, 10, 17, 17, 20, 24, 30};public static int cutByDP(int n) {int[] r = new int[n + 1];for (int i = 1; i <= n; i++) {int q = -1;for (int j = 1; j <= i; j++)q = Math.max(q, p[j - 1] + r[i - j]);r[i] = q;}return r[n];
}

整理完毕，完结撒花~ 🌻

参考地址：

1.算法-动态规划 Dynamic Programming–从菜鸟到老鸟，https://blog.csdn.net/u013309870/article/details/75193592

2.告别动态规划，连刷40道动规算法题，我总结了动规的套路，https://blog.csdn.net/hollis_chuang/article/details/103045322